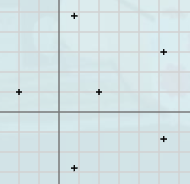
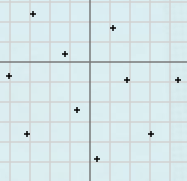
定義域２次元、値域１次元の滑らかな関数を推定する課題に対応します。特に、極小点、極大点のような局所的挙動を調べるのに有効です。
使い方：
- x 座標 y 座標は、graph の上をクリックすることで入力できます。すでにある点の上をクリックし、ドラッグすると移動できます。移動せずに離すと、点を消せます。 clear ボタンで全ての点を消せます。
- グラフの視野は、右ボタンのドラッグで移動できます。また、+ および - ボタンで拡大、縮小できます。fix ボタンによって、罫線の一つを中心に移動できます。
- 設定された x、y のデータは text に入ります。
- x、y の入力は "text" からもできます。行毎に x 座標 y 座標の順で入れて下さい。一個以上の空白またはコンマで区切ります。
- z の入力は、実データなどに基づく text への手入力と、関数を利用する自動入力の両方が可能です。
- ドロップダウンリストである samples から選択することにより、予め用意された関数を指定することが可能です。この関数は、formula に表示されます。
- samples から選ぶ以外に、同様の形式で formula に書き込んで指定できます。
- 実験など、実現象のデータは、そもそも関数が不明なので、個々のデータの計測値を手入力します。 この場合は formula を空白にしておいた上で、text の各行で x, y に続く第３の数値として入れて下さい。
- 特定の個数（3, 6, 10, 15, 21, 28, 36, 45）個に達すると、各点の推定値を自動計算し、estimations_z に表示します。 この際に根拠とする推定式は estimated polynomial に表示され、推定に際しての計測点（x, y）のセットの適切度の指標を index に表示します。 さらに、マウスを graph 上で（クリックせずに）動かすことにより、推定値と index のプレビューを estm_z preview と index preview に表示します。
- ord. のプルダウンメニューでは、データの数に対して計算可能な最大の次数が自動的に選ばれます。例えば「3(10)」という表示は、次数 n が３、 この条件で計算可能なデータ数 m の最低値（これは項の数に等しい）が 10 であることを意味し、m に対し、m ≧ (n+1)*(n+2)/2 を満たす、最大の n が設定されます。
赤い領域は数種の課題を保持しています。これは、x,y の値から、関数値 z を導くものです。これは、黄色の領域にある窓を通じて問い合わせることもできます （xyset に x と y の値を設定し、→ ボタンを押すと、formula に表示された式にこれらを代入した結果が zget に表示されます）。
青い領域はソルバーですが、ここから赤い領域に問い合わせているのは、黄色の領域からもアクセスできる、せいぜい数点の値の情報のみです。 これは、formula の式を得ているのではなくて、個々の x,y 対に対応した値を得ているに過ぎません。
まずは使ってみましょう。バナナ関数の極小点を求めるには次のようにします。
- samples のプルダウンメニューで、banana を選びます。
- graph の領域をランダムにクリックし、15個の点を入れます。
- たったこれだけです。特に運が悪くなければ、マウスを（クリックせずに）graph 上の（1, 1）の格子点に合わせることで、estim_z preview に "0" が表示され、これが極小になっているはずです。
解説：
１次元関数のフィッティングをご前回は説明しましたが、今回２次元です。ただし、広域で合わせるのではなく、２次曲面で近似される極小点付近のみの解析を狙います。
極小点の周辺で多項式展開すると、２次までの近似式は、
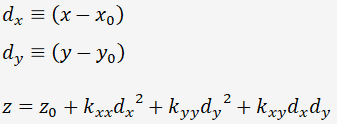
となりますが、このままでは線形の最小二乗法には適しません。 前回ご説明したように、個々の関数はどんな形でも良いが、それらに係数を掛けた一次結合でないといけないのでした。 線形の最小二乗法に適するのは、次の形です。
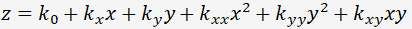
こちらは、原点を中心に展開したものとも言えます。
これは２次の場合ですが、他の次数についても同様に多項式展開しています。
【極小点など、ローカル座標への変換】
２次の場合であれば、両式の x, y の各一次の項、および定数項を比べると、次の関係が言えます。
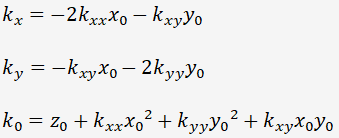
実際に欲しいのはこの逆の変換です。連立一次方程式として上の式を解くと、次のようになります。
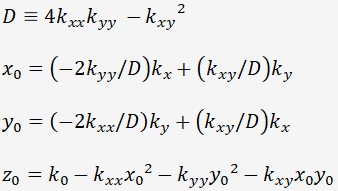
計算の流れは、前回行ったと同じように、測定点と測定値の条件から一般逆行列を作って、
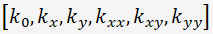を求め、これを変換して、
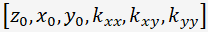を得ることです。両方のベクトルに共通する
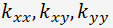については特に変換する必要はありません。３次以上では、このように簡単ではなくなります。 奇数次の場合など、そもそも最大値や最小値がない場合もあるので、極と思われる点の付近で数値的に解析するのが良いでしょう。
【指標について】
x,y と、その点数だけのデータの標準偏差
、また、後で定義する係数 
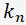から次の式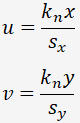
で導かれる u, v から、次数だけの項を揃えた行を作ります。例えば２次であれば、
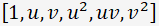の６因子ベクトル、
３次であれば、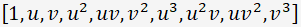
の10 因子ベクトルです。
これを測定点の数だけ並べたマトリクスを A 、測定点の数を I とすると、今回の指標の定義は、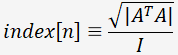
ただし、n=0 から n=8 までの
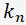は、
[1,1,
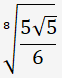,1.4, 1.6, 1.85, 2.1, 2.25, 2.4]。
この係数は、最低点数で最適である場合の index 値が１に近くなるように決めました。n=2 には根拠がありますが、他は経験的なエイヤッです。さて、推定すべき目標もさることながら、この指標に着目して色々試すのは面白いです。 ２次式の推定は、最低６点でできるのですが、６点でもそれ以上でも、指標がゼロになってしまう点の置き方というのがあります。 それは、円や楕円（斜めに長いものを含む）が仮定される線上に全ての点が配置された場合です。
これは、茶碗や皿の淵の上に全ての測定点があった場合、曲率について、それが凹んでいるのか、むしろ、山になっているのかという肝心な情報が欠けてしまうことから納得できます。
それでは、指標が大きい理想的な配置とはどんなものでしょうか？ 私は最初、三角形の頂点と、各辺の中点という、FEM の二次要素のような配置が良いのではないかと想像しました。
調べてみると、それは悪くはないが、特に良くもない。それでは最良の配置は何かというと、正五角形の頂点とその中心に配置した場合でした。 さらに、そのアフィン変換でも同じような結果になります。この配置を以後「梅鉢」と呼ぶことにします。
先ほどの指標の定義は、この最良の配置を６点で行った場合、値が１になるように調整したものです。
３次式の推定をするための良好な指標を探したところ、大体二重の円の内周に３個、外周に６個、内周とも外周とも言えない微妙な位置に１個の点を配置した場合がほぼ最良と わかりました。繋げると、電話会社のマークに似ているかも。
より高次では、適当に点を置いて、心配なら、多少余分にサンプリングしておけば良いと思われます。なにせ、「一般逆行列」ですから。
あるいは、指標を参考にして実験を計画してみて下さい。指標の取得は、実際に実験データを得る以前に可能です。
【有限次数多項式の場合】
一般に関数による近似というのは、狭い範囲ではそこそこ合っても、視野を広くしてしまうとずれが生じるものです。 だから、極小点の探索では、推定された極小点の近くに、次第に計測点を集中させる必要があり、少なくとも、その点を囲うように、点を配置するべきです。
ところが、今回サンプルとして挙げた関数は何れも、有限次数の多項式なので、十分な次数で推定した場合、 極小点と全く関係ないサンプリング点からでも、結構正確な値が得られてしまいます。
【変数の数と次数に対応した項の数】
次の表に整理されます。
表：項の数
| 変数の個数 | 次数 | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 |
| 3 | 4 | 10 | 20 | 35 | 56 | 84 | 120 | 165 |
| 4 | 5 | 15 | 35 | 70 | 126 | 210 | 330 | 495 |
| 5 | 6 | 21 | 56 | 126 | 252 | 462 | 792 | 1287 |
| 6 | 7 | 28 | 84 | 210 | 462 | 924 | 1716 | 3003 |
| 7 | 8 | 36 | 120 | 330 | 792 | 1716 | 3432 | 6435 |
| 8 | 9 | 45 | 165 | 495 | 1287 | 3003 | 6435 | 12870 |
項の数を示すこの表の意味ですが、例えば変数が２個（x と y）で３次の式なら、
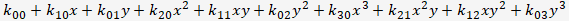
となり、10個。また、変数が３個（x, y, z）で２次の式なら、
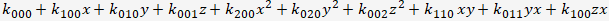
となり、やはり10個となります。次数と変数の個数を入れ替えても同じ個数になり、表を斜めに見ると二項数列になっていることに気付きます。
変数が２個である、このページの課題においては、項の数は、次数 n に対して (n+1)*(n+2)/2 になっていますが、これは n+1 に対応する三角数であるとも言えます。
【最適化手法としての意義（２ステップ手法）】
表で real_z として入れられるのは、生データと言えます。それに対して、estimations_z として出力しているのは、多項式として近似した推定値です。
結局これは、生データを多項式で近似する第１ステップと、それをもとに極小値等を解析する第２ステップとに分けた解析手法と言えます。
第１のステップでは、実験等の試行を１回行う毎に、それなりの工数、費用が必要であり、これを減らすことが求められます。 直交化表など、過去にも解析手法はありましたが、今回の方法は、理論上最小の情報量でこれを実施できるので、必ず優れているはずです。 何より、追加実験で、過去の実験データも取り込める点が大きなメリットだと思っています。
多項式近似ができた後は、これを解析する必要がありますが、これについてはコンピュータのコストも下がった昨今、ほとんど論じるべき問題ではないでしょう。